cosmology – Urmila Chadayammuri

CosmosVR – A Virtual Reality Exploration of a Cosmological Simulation

March 6, 2019uc24 Leave a Comment

We made a Virtual Reality cosmology show!

This winter break, a friend took me to the Adler Planetarium in Chicago. This is one of the best space museums in the country, and had fascinating exhibits and movies about planets within and outside the Solar System, and the history of our attempts to explore them, going all the way back to Medieval timekeeping instruments. But when we got to the cosmology exhibit, my heart sank. The Big Bang! Dark matter! Dark energy! The fact that we can measure the how fast the Universe was expanding eight billion light years ago! How it looked thirteen billion years ago! Nothing. Some lame-ass screens full of text. None of the images, the mind-blowing technology, the methods we have to use to figure out what the Universe looks on the largest scales of space and time.

And Adler is not alone. Every museum cosmology exhibit I’ve been to has been woefully lacking.

So at the MIT VR Hackathon last month, I made a pitch to create a museum/planetarium show about extragalactic space. Self-driving car programmer Paul, computational biologist Diego, and the most impressive undergrad I have ever met, Beste, got on board. We loaded data from the Illustris simulation and visualised it in Unity (no small task). If you’re in the room with the VR headset and controller, you can fly around the space, toggle between views of the stars, gas and dark matter, and zoom in to see an individual galaxy in high resolution. For those of you further away, we recorded this demo, with a little spacey music and educational voiceover from yours truly.

I was already over the moon (ha) because I had daydreamed of this for almost a year and it came together in two days. And because we were such a day dream, and working on it was so much fun. But then we won the Data Visualization prize (thanks Fidelity!). And a mentorship offer from _underscore VC. And support from Rus Gant of Harvard and Scott Greenwald of the MIT media lab to develop this further.

So now I’m really excited about all the places we’ll go! I still have to finish my PhD, hopefully in about a year. But in the meantime, you can experience the show at the Cambridge Science Festival on April 13 – just grab your free tickets.

We’re adding more features, like data sonification and more interaction and would love to bring the show to museums and planetariums around the country (heck, world, if you’re reading this abroad!). So if you have ideas and/or contacts, please do hit me up.

#Sparknotes: Black Holes as Chaotic Eaters

September 1, 2016uc24 Leave a Comment

Chaotic cold accretion onto black holes

Gaspari, Ruszowski and Oh, 2013

This paper describes a set of very high resolution, idealized simulations of a supermassive black hole (SMBH) in the central (cD) galaxy of a massive cluster. Since the goal is essentially to challenge the current near-universal use of the Bondi accretion model in simulations, let’s start with the key equation:

Setup Start with a simple NFW dark matter halo, a de Vaucouleurs stellar distribution, gas that traces the gravitational potential and a SMBH, all with masses similar to the observed galaxy group NGC 5044. All of these are modelled in an adaptive mesh grid overlaid on a box of side 52kpc for a total time of 40 Myr. With upto 44 levels of refinement, the simulation resolves sub-parsec scales around the central black hole.

Mass accretion onto the black hole, normalized by Bondi prediction.

Varying physics models

The initial setup thus consists of an ideal gas contracting under gravity. This results in adiabatic, isotropic, smooth accretion of warm gas, identical to the analytic model of Bondi (1952). Indeed, the (numerically) observed accretion in this case exactly matches Bondi’s prediction, since the solid line in Fig 1b is essentially = 1 throughout. What is the dashed line, you ask? Well, that is the accretion rate you would measure if you evaluated the parameters in the Bondi equation as an average over a cluster-centric radius of 1-2 kpc, instead of at the Bondi radius (85pc in this case). In other words, computing gas density and sound speed as an average over large cells overestimates the accretion rate.

The simulations sequentially complicate the physics.

First they add cooling, which occurs due to atomic transitions in the ICM. Observed cluster ICMs tend to be quite enriched in metals, mostly due to ejecta from supernovae. They assume the metallicity of the cluster gas to equal that of the sun, which I thought was generous but is actually supported by Chandra observations (e.g. Vikhlinin et al 2005). The accretion is now boosted by over two orders of magnitude. Of course, the simulation doesn’t model star formation; if it did, a lot of this centrally accreted gas could actually be converted into stars, so we would observe very large star formation rates in over very short time scales in the central galaxies of clusters. We d not.

Next, they add turbulence by “stirring” the gas on large scales (lol 4kpc; this is just about the resolution of our cosmological simulation. It’s so relieving to see that someone is actually probing the smaller regions so that our sub-grid models aren’t full of hot air.)(I’m sorry I can’t help these things.) In reality turbulence can be induced by galaxy motions through the viscous ICM, galaxy-galaxy mergers, AGN and stellar feedback, etc. And this is where things start to look really different.

You now see a slice of the temperature profile of the gas. Adding the metal cooling, as mentioned above, decreases the temperature in the core by over 4 orders of magnitude, but retains the spherical symmetry and isotropy. Adding turbulence creates very cold filaments on very large scales. The accretion is on average as high as in the cooling-only scenario, but with more fluctuations.

Lastly, they consider global heating. In a real cluster, this could come from cosmic rays, AGN feedback, massive stellar feedback, etc. This suppresses the star formation somewhat from the previous case, but the “boost factor” with respect to the Bondi prediction is just under 100 by the end of the simulation. The filaments induced by turbulence are not broken up or significantly heated up.

In summary: accretion of gas onto the supermassive black holes at the centres of galaxy clusters is cold, chaotic and filamentary. Averaged over tens of megayears, the boost factor with respect to the Bondi model is just under 100, compared to the prevalent norm of 100-400.

#Sparknotes: AGN

August 15, 2016uc24 Leave a Comment

So excited about this fall! I get to implement a new subgrid model for accretion onto, and feedback from, active galactic nuclei (AGN) at the centres of clusters in a cosmological simulation we develop here at Yale.

Developing subgrid models (and numerical approximations in general) is an art as much as a science. On the one hand, you need to reproduce large-scale, observable phenomena, like star formation histories, stellar masses, stellar and metallicities, and dark and visible substructure. On the other, you want your input parameters to be motivated by plausible underlying physics.

Fig 1 from Urry and Padovani, 1995

AGN are a pesky beast. They consist of a supermassive black hole (SMBH) at the core, or nucleus, of a galaxy, surrounded by a hot disk of infalling matter. Since the material in the disk is unlikely to have falling in on a radial trajectory, it settles in a rotating disk around the black hole. Friction between layers of the disk heat it up to tens of millions of Kelvin, so that if you catch an AGN at the correct angle, it is bright in the X-ray. More often than not, due to geometric reasons, you’ll end up seeing dust-obscured AGN, which are bright in the radio. That’s a two-line summary of the Unified Model of AGN.

This obscuration, combined with the final parsec problem, is the main reason AGN are so pesky. Stuff falls onto black hole, aggravates it, isothermal heat ejections and mechanical jets arise! But what sort of stuff can fall into the black hole? Why does that cause it to spit stuff out? How exactly does it eject this energy? How far does the energy travel, and how does it interact with gas on its way (more specifically, the Intra-Cluster Medium or the ICM)?

There has been a sea of observations and theoretical models on this topic in the last few decades, and I’m just starting to dip my toes in it. Here’s a summary of the papers I’ll review in the next months.

How is energy transported within an accretion disk? How do the viscosity, density and temperature of the gas in the accretion disk determine whether energy transport is dominated by radiation, advection or convection? What does each of these processes look like? Advection-Dominated Accretion around Black Holes – Narayan, Mahadevan and Quataert, 1998
How exactly does the gas fall onto the black hole? How cold does it have to be? Does this depend on whether the gas is in filaments or clouds, and how those may be oriented? Growing supermassive black holes by chaotic accretion – Gaspari et al, 2013
The simulation I work with extracts clusters of galaxies from a cosmological box. This captures things idealized/isolated cluster simulations cannot, like smooth accretion of gas from filaments and mergers of clusters. Accretion during the merger of supermassive black holes – Armitage and Natarajan, 2002
Several self-regulating mechanisms have resulted in tight relations between galaxies and the supermassive black holes that live in their centres. Accreting supermassive black holes in the COSMOS field and the connection to their host galaxies – Bongiorno et al, 2012.
- Also, Self-regulated Growth of Supermassive Black Holes in Galaxies as the Origin of the Optical and X-Ray Luminosity Functions of Quasars – Wyithe and Loeb, 2003

Simulating the First Dwarf Galaxies and Globular Clusters

July 20, 2016uc24 Leave a Comment

A Common Origin for Globular Clusters and Ultra-faint Dwarfs in Simulations of the First Galaxies

Massimo Ricotti, Owen H. Parry and Nickolay Y. Gnedin

This paper presents the results of simulations of four cosmological boxes, each 1 Mpc/h a side, using the Adaptive Refinement Tree (ART) technique. The adaptive refinement scheme creates finer spatial and temporal resolutions in regions of high density, where the physics is more interesting. In the highest-resolution run, the authors resolve individual star particles as small at 40 $M_\odot$ , at sub-parsec sizes. The numerical simulation ends at z ~ 9, sufficient to make predictions about what the James Webb Space Telescope would see. Afterwards, an analytical prescription extrapolates what the galaxies found at z=9 would look like today, and comparisons are made to dwarf galaxies and globular clusters in the Local Group.

The physics implementation here is very neatly explained and physically motivated. Stars form whenever a gas cell meets certain criteria of metallicity, number density and molecular hydrogen fraction. There are two sets of prescriptions, corresponding to metallicity requirements for Pop III and Pop II stars. Unless the gas cell is of the minimum mass, i.e. 40 $M_\odot$ , it is converted into a stellar particle, which is understood as a population of stars following the Chabrier IMF. Feedback occurs in the form of supernova (SNe) explosions 3 Myr after star formation has occurred in a given cell – this timescale corresponds to the main sequence lifetime of an 8 $M_\odot$ star. This releases $10^{51}$ ergs of thermal energy into the neighbouring cells, on time scales that range from 0 (for Pop III hypernovae) to 35 Myr (for Pop II supernovae). The feedback also serves to enrich the gas with metals.

Finally, substructure is identified at every time step using the friend-of-friends (FoF) algorithm and refined using SubFind. The high-res simulation produced galaxies as small as 2.8 $\times 10^5 M_\odot$ , comparable to ultra-faint dwarfs today! Btw, I was elated that someone finally explained linking length, which is key to FoF! Particles are considered linked if their separation is less than

(linking length)*(mean separation between particles in the box)

The group catalogues are then used to construct merger trees.

At z = 9, they find that many galaxies have gas disks, but stars still form spheroids –

This makes sense if a spheroidal gas cloud was cool enough for star formation before dissipative processes turned it into a disk.

What do the orbits of the stars look like? Defining circularity as the angular momentum of a star particle in the direction of the mean angular momentum of the galaxy, divided by that of a particle of that mass moving on a circular orbit. The star particles in the simulated galaxies are consistent with non-rotating spheroids, i.e. symmetric distributions of circularity peaking at zero. In some galaxies, the mean circularity is positive, indicating that at least some stars are undergoing some rotation. No difference between metal rich and metal poor stars, divided at [Fe/H] = -1.5.

How big are the galaxies? Half-light radius $r_h$ computed at 100 different viewing angles, error bars represent range between 10th and 90th percentile of measured values for each. Unlike observations in Local Group, where $r_h$ scales with luminosity/stellar mass, in the simulation there is a large spread in $r_h$ at fixed stellar mass. That said, a lot can happen between z = 9 and the present day. If tidal stripping, for example, occurs at a rate inversely proportional to the density of the dwarf galaxy, more extended low-mass galaxies at high z would be smaller by z=0. Patience – this comes a couple sections later!

Of the ten most compact objects, 5 are DM dominated and 5 baryon-dominated. In fig 6, this is seen as a wide range in pseudo mass-to-light ratios at a fixed dynamical mass. There is, nevertheless, an apparently bimodal distribution – one where mass/light hovers around 10, and another around 10,000.

The money plot:

The three panels correspond to three different values adopted for star formation efficiency, ranging from 1-100%. To quote the authors, “luminosity of dwarfs increases by about a factor of two whenis increased by a factor of 100”; i.e. the qualitative results are depend very weakly on the assumed 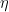$\eta$ (which is excellent, since this quantity is still poorly constrained by observations)! The grayscale is the log of the stellar mass to dark matter mass.

Takeaway: the simulation self-consistently forms several objects with half-light radii ranging from 1-150 pc and stellar-to-dark matter ratios ranging from 1:1,000 to 10,000:1! The latter systems live in the top left corner of each plot, and are consistent with the mass-to-light ratios observed in globular clusters today. The more dark-matter dominated systems, on the other hand, would be the progenitors of dwarf galaxies.

[The plots in this paper are so damn nice. Like, they really know the physics point they’re trying to get across.]

Finally, the paper analytically calculates what these high-redshift compact objects would look like in the Local Universe, and compare it to observations.

Overall, it seems to me that the dwarf galaxies in the simulation don’t fit observations nearly as well as the globular clusters do – the simulation+analytic evolution produce dwarfs that are more compact, have smaller velocity dispersions, and with a smaller range of masses than observed. That said, the 13 billion years between the end of the simulation and the present day are very complex to model, and the fact that the predictions are so close to the observations is pretty impressive!

Ultimately the conclusion is that globular clusters and dwarf galaxies form through the same processes in the very early universe. How do you form very compact, baryon-dominated systems at high redshifts, though? I might have to re-read the paper to get this one.